problem
stringlengths 18
2.25k
| gt
stringlengths 1
173
|
|---|---|
62. The clock strikes twelve
- Grandfather's clock strikes six times in thirty seconds. How many seconds will it take to strike twelve times? - asked the Black Queen.
- Of course, in sixty seconds! - exclaimed Alice. - Oh no! - she corrected herself. - I was wrong. Please wait, I will give the correct answer now!
- Too late! - triumphantly pronounced the Black Queen. - What's said can't be unsaid!
What is the correct answer?
|
66\mathrm{}
|
## 29. Umbrella
One Saturday evening, two brothers, Jean and Pierre, exchanged their observations about the behavior of their neighbor, Madame Martin. They agreed that every Sunday she goes out of the house once (and only once), that in two out of three cases she takes an umbrella with her, and therefore even on good weather days, she goes for a walk with an umbrella half the time. However, Jean believed that on rainy days she never forgets to take an umbrella, while Pierre, on the contrary, claimed that sometimes she goes for a walk without an umbrella even on rainy days.
Which of the brothers, in your opinion, is right and which is wrong, if in their region, on average, half of the days are rainy?
|
Pierre
|
Given a real number $ c > 0$, a sequence $ (x_n)$ of real numbers is defined by $ x_{n \plus{} 1} \equal{} \sqrt {c \minus{} \sqrt {c \plus{} x_n}}$ for $ n \ge 0$. Find all values of $ c$ such that for each initial value $ x_0$ in $ (0, c)$, the sequence $ (x_n)$ is defined for all $ n$ and has a finite limit $ \lim x_n$ when $ n\to \plus{} \infty$.
|
c \geq 2
|
Example 3 Choose 1 young man and 1 young woman from each of the four groups to perform a circle dance, with the rule that men and women must alternate, and two people from the same group cannot be adjacent. How many different team formation variations are there?
|
12
|
6. (6 points) On the blackboard, there is a number in the form of $7777 \cdots 77$. Each time, erase the last digit, multiply the remaining number by 3, and then add the digit that was just erased. Continue operating on the new number in the same way, and the final number obtained is . $\qquad$
|
7
|
3. For which values of the variable $x$ is the value of the function
$$
f(x)=\log _{\frac{1}{2}}\left(\frac{x}{x+2}-\frac{1}{x}\right)
$$
negative?
|
x\in(-\infty,-2)\cup(-\frac{2}{3},0)
|
Problem 8.1.1. Dima and Seryozha were picking berries from a raspberry bush, on which 900 berries grew. Dima alternated his actions while picking: he put one berry in the basket and ate the next one. Seryozha also alternated: he put two berries in the basket and ate the next one. It is known that Dima picks berries twice as fast as Seryozha. At some point, the boys had picked all the raspberries from the bush.
Who of them ended up putting more berries in the basket? What will the difference be?
|
100
|
2. Let $A_{n}$ and $B_{n}$ be the sums of the first $n$ terms of the arithmetic sequences $\left\{a_{n}\right\}$ and $\left\{b_{n}\right\}$, respectively. If $\frac{A_{n}}{B_{n}}=\frac{5 n-3}{n+9}$, then $\frac{a_{8}}{b_{8}}=$ $\qquad$ .
|
3
|
A gardener plants three maple trees, four oaks, and five birch trees in a row. He plants them in random order, each arrangement being equally likely. Let $\frac m n$ in lowest terms be the [probability](https://artofproblemsolving.com/wiki/index.php/Probability) that no two birch trees are next to one another. Find $m+n$.
|
106
|
For $a>1$, let $f(x)=\int_{x}^{ax} \sqrt{1-t^2} \,dt\ \left(0\leq x\leq \frac{1}{a}\right).$
(1) Evaluate $f\left(\frac 1{a\right)}+\int_0^{\frac{1}{a}} \sqrt{1-t^2}\ dt.$
(2) Find the value of $M$ such that $f(x)$ has maximum value $M$ at $x=\frac{\sqrt{3}}{2a}.$
|
\frac{\pi}{4}
|
6. (8 points) On the board, 34 ones are written. Every minute, Karlson erases two arbitrary numbers and writes their sum on the board, and then eats a number of candies equal to the product of the two erased numbers. What is the maximum number of candies he could have eaten in 34 minutes?
|
561
|
3.46 The path from $A$ to $B$ is traveled by a passenger train 3 hours and 12 minutes faster than by a freight train. In the time it takes the freight train to travel from $A$ to $B$, the passenger train travels 288 km more. If the speed of each train is increased by $10 \mathrm{km} / \mathrm{h}$, the passenger train will travel from $A$ to $B$ 2 hours and 24 minutes faster than the freight train. Determine the distance from $A$ to $B$.
|
360
|
A6. A two-digit number ' $a b$ ' is multiplied by its reverse ' $b a$ '. The ones (units) and tens digits of the four-digit answer are both 0 .
What is the value of the smallest such two-digit number ' $a b$ '?
|
25
|
34.2. Find all functions $f(x)$ that are defined for $x \neq 1$ and satisfy the relation
$$
f(x) + f\left(\frac{1}{1-x}\right) = x
$$
|
f(x)=\frac{1}{2}(x+1-\frac{1}{x}-\frac{1}{1-x})
|
266. When division is exact. For which positive integer $n$ will the quantity $n^{4}+n^{2}$ be divisible by $2 n+1$?
|
2
|
Petya wrote a hundred-digit number $X$, in which there are no zeros. The fifty-digit number formed by the first fifty digits of the number $X$, Petya called the head of the number $X$. It turned out that the number $X$ is divisible by its head without a remainder. How many zeros are in the quotient? #
|
49
|
4. The condition that can determine quadrilateral $ABCD$ is a rhombus is ( ).
(A) Diagonal $AC$ bisects diagonal $BD$, and $AC$ $\perp BD$
(B) Diagonal $AC$ bisects diagonal $BD$, and $\angle A$ $=\angle C$
(C) Diagonal $AC$ bisects diagonal $BD$, and bisects $\angle A, \angle C$
(D) Diagonal $AC$ bisects $\angle A, \angle C$, and $\angle A$ $=\angle C$
|
D
|
1. Natural numbers a and b are such that 5 LCM $(a, b)+2$ GCD $(a, b)=120$. Find the greatest possible value of the number a.
|
20
|
52. As shown in the figure, in quadrilateral $A B C D$, $A B=7, B C=24, C D=20, D A=15, \angle B=90^{\circ}$, then the area of quadrilateral $A B C D$ is . $\qquad$
|
234
|
The cities of Coco da Selva and Quixajuba are connected by a bus line. Buses leave Coco da Selva for Quixajuba every hour, with the first one departing at midnight on the dot. Buses leave Quixajuba for Coco da Selva every hour, with the first one departing at half past midnight. The bus journey takes exactly 5 hours.
If a bus leaves Coco da Selva at noon, how many buses coming from Quixajuba does it encounter during the journey?
Figure 21.2
Figure 21.3
Figure 21.4
|
10
|
3. Find all positive solutions of the system of equations.
$$
\left\{\begin{array}{c}
x_{1}+x_{2}=4 x_{3}^{2} \\
x_{2}+x_{3}=4 x_{4}^{2} \\
\cdots \\
x_{2015}+x_{2016}=4 x_{2017}^{2} \\
x_{2016}+x_{2017}=4 x_{1}^{2} \\
x_{2017}+x_{1}=4 x_{2}^{2}
\end{array}\right.
$$
In your answer, specify the value of \( x_{1} \). If there are multiple correct answers, list them in any order separated by a semicolon.
|
0.5
|
150. Two shooters shoot at a target. The probability of a miss with one shot for the first shooter is 0.2, and for the second shooter it is 0.4. Find the most probable number of volleys in which there will be no hits on the target, if the shooters will make 25 volleys.
|
2
|
Suppose that $n$ is a positive integer and that the set $S$ contains exactly $n$ distinct positive integers. If the mean of the elements of $S$ is equal to $\frac{2}{5}$ of the largest element of $S$ and is also equal to $\frac{7}{4}$ of the smallest element of $S$, determine the minimum possible value of $n$.
|
5
|
## Task B-4.2.
Determine all natural numbers $x, y$ for which $1!+2!+\cdots+x!=y^{2}$.
|
(x,y)\in{(1,1),(3,3)}
|
39. Calculate: $2379 \cdot 23782378-2378 \cdot 23792379$.
|
0
|
18. (17 points) Let $a_{1}, a_{2}, \cdots, a_{n}$ be a permutation of the integers 1, 2, $\cdots, n$, and satisfy the following conditions:
(1) $a_{1}=1$;
(2) $\left|a_{i}-a_{i+1}\right| \leqslant 2(i=1,2, \cdots, n-1)$.
Let the number of such permutations be $f(n)$. Find the remainder when $f(2010)$ is divided by 3.
|
1
|
## Problem 3
i) In the exercise $8+10 \times 2+2 \times 8: 4$ place a pair of round brackets so that you obtain:
a) the smallest possible number (3 points)
b) the largest possible number (2 points)
ii) Calculate $3 m+5 n+4 p$, given that $m+n=25$ and $n+2 p=65$. (2 points)
|
205
|
4. The quiz participants were asked four questions: 90 participants answered the first question correctly, 50 answered the second, 40 answered the third, and 20 answered the fourth, and no one was able to answer more than two questions correctly. What is the minimum number of participants in the quiz under these conditions?
|
100
|
4. Find all prime numbers whose decimal representation has the form 101010 ... 101 (ones and zeros alternate).
|
101
|
## Task 3/70
It is $x^{0}=1$ and $0^{x}=0$ for $x \neq 0$. What is the value of $\lim _{x \rightarrow 0} x^{x}$ ?
|
1
|
[ [product of the lengths of the segments of chords and the lengths of the segments of secants ] [ Radical axis $]$
Two circles intersect at points $A$ and $B$. Chord $C D$ of the first circle has a common point $M$ with chord $E F$ of the second circle. It is known that $B M=2, A B=3 C M=9 E M, M D=2 C M, M F=6 C M$. What values can the length of the segment $A M$ take?
|
4or1
|
N5. Find all positive integers $x, y, z$ such that
$$
45^{x}-6^{y}=2019^{z}
$$
|
(2,1,1)
|
13th APMO 2001 Problem 2 Find the largest n so that the number of integers less than or equal to n and divisible by 3 equals the number divisible by 5 or 7 (or both). Solution
|
65
|
7.2. Petya wrote down all natural numbers from 1 to $n$ in a row on the board and counted the total number of digits written. It turned out to be 777. What is $n$?
|
295
|
12. As shown in the figure, a rectangular lawn is divided into three parts. It is known that the second plot is 10 meters wider than the first plot. The area of the second plot is 1000 square meters, the third plot is 4 meters narrower than the first plot, and the area of the third plot is 650 square meters. Therefore, the area of the first plot is ( ) square meters.
|
750
|
Among four numbers, the first three form an arithmetic sequence, the second three form a geometric sequence. The sum of the first and fourth number is 37, the sum of the second and third is 36. Which are these four numbers?
|
12,16,20,25\quad
|
4. Let $a, b$, and $c$ be three distinct real numbers. Find the minimum possible value of the expression
$$
\left|\frac{a}{b-c}\right|+\left|\frac{b}{c-a}\right|+\left|\frac{c}{a-b}\right|
$$
if it exists, as well as all triples $(a, b, c)$ for which this value is achieved.
|
2
|
2. Determine all values of the real parameter $k$ such that:
$$
(\forall x \in \mathbb{R})\left(k x^{2}-4 k x+k^{2}+2 k-3>0\right)
$$
|
k\in(3,\infty)
|
Let $a$ be a positive constant. Evaluate the following definite integrals $A,\ B$.
\[A=\int_0^{\pi} e^{-ax}\sin ^ 2 x\ dx,\ B=\int_0^{\pi} e^{-ax}\cos ^ 2 x\ dx\].
[i]1998 Shinsyu University entrance exam/Textile Science[/i]
|
B = \frac{1}{2} \left( \frac{1}{a} + \frac{a}{a^2 + 4} \right) (1 - e^{-a\pi})
|
1. Let $a=(x+1)(x+2)(x+3)(x+4)$, $b=(x-4)(x-3)(x-2)(x-1)$. Then $a-b$ equals ( ).
(A) $20 x^{3}+50 x$
(B) $2 x^{3}+5 x$
(C) $20 x^{4}+100 x^{2}$
(D) $20 x^{3}+100 x$
|
D
|
# Task 4. (12 points)
A shooting tournament involves several series of 10 shots each. In one series, Ivan scored 82 points, as a result of which the average number of points he scored per series increased from 75 to 76 points. How many points does Ivan need to score in the next series of shots to make the average number of points scored per series equal to 77?
|
84
|
## Task 4 - 170824
Dieter tells his classmates:
"My brother Fritz is only half as old as I am. If you multiply the number of his years by itself, you get my father's age. My mother is three years younger than my father. All together, we are 87 years old."
Determine the age of all 4 people! (Only the completed years of life are to be considered.)
|
36,6,12,33
|
Let a sequence $(x_n)$ satisfy :$x_1=1$ and $x_{n+1}=x_n+3\sqrt{x_n} + \frac{n}{\sqrt{x_n}}$,$\forall$n$\ge1$
a) Prove lim$\frac{n}{x_n}=0$
b) Find lim$\frac{n^2}{x_n}$
|
\frac{4}{9}
|
6.27 In triangle $A B C$, $\angle A=2 \angle B$, $\angle C$ is an obtuse angle, and the three side lengths $a$, $b$, $c$ are all integers. Find the minimum perimeter and provide a proof.
(20th United States of America Mathematical Olympiad, 1991)
|
77
|
4. The sequence $\left\{x_{n}\right\}$ satisfies $x_{1}=\frac{1}{2}, x_{k+1}=x_{k}^{2}+x_{k}$. Then the integer part of the sum $\frac{1}{x_{1}+1}+\frac{1}{x_{2}+1}+\cdots+\frac{1}{x_{200 B}+1}$ is $\qquad$
|
1
|
2. In a math competition, 3 problems are proposed, each of which is scored with an integer between 0 and 7 (inclusive). It is known that, no matter which two participants are chosen, there is at most one problem on which these two have obtained the same score (for example, there are no two participants whose scores on the three problems are 7, 1, 2 for the first and 7, 5, 2 for the second, but there could be two participants whose scores are 7, 1, 2 and 7, 2, 1). What is the maximum number of participants in the competition?
|
64
|
1. 10 people are playing musical chairs with $n$ chairs in a circle. They can be seated in 7! ways (assuming only one person fits on each chair, of course), where different arrangements of the same people on chairs, even rotations, are considered different. Find $n$.
|
4
|
2.136. $\frac{1-b}{\sqrt{b}} \cdot x^{2}-2 x+\sqrt{b} ; \quad x=\frac{\sqrt{b}}{1-\sqrt{b}}$.
2.136. $\frac{1-b}{\sqrt{b}} \cdot x^{2}-2 x+\sqrt{b} ; \quad x=\frac{\sqrt{b}}{1-\sqrt{b}}$.
|
0
|
5. Find all surjective functions $f: \mathbf{N}_{+} \rightarrow \mathbf{N}_{+}$ such that for any $m, n \in \mathbf{N}_{+}$ and any prime $p$, $f(m+n)$ is divisible by $p$ if and only if $f(m) + f(n)$ is divisible by $p$.
|
f(n)=n
|
Example 3. Find the integral $\int\left(1-\frac{1}{x^{2}}\right)^{2} d x$.
|
x+\frac{2}{x}-\frac{1}{3x^{3}}+C
|
Segment $K L$ is the diameter of a certain circle. Through its endpoints $K$ and $L$, two lines are drawn, intersecting the circle at points $P$ and $Q$, respectively, lying on the same side of the line $K L$. Find the radius of the circle if $\angle P K L=60^{\circ}$ and the point of intersection of the lines $K P$ and $Q L$ is 1 unit away from points $P$ and $Q$.
|
1
|
Example 11 Let $p(x)$ be a polynomial of degree $3n$, such that $P(0)=P(3) \cdots=P(3n)=2, P(1)=$ $P(4)=\cdots=P(3n-2)=1, P(2)=P(5)=\cdots=P(3n-1)=0, P(3n+1)=730$. Determine $n$.
(13th US Olympiad Problem)
|
4
|
$4 \cdot 31$ Real numbers $x_{1}, x_{2}, x_{3}, x_{4}, x_{5}$ satisfy the system of equations
$$
\left\{\begin{array}{l}
x_{1}+x_{2}+x_{3}=a_{1}, \\
x_{2}+x_{3}+x_{4}=a_{2}, \\
x_{3}+x_{4}+x_{5}=a_{3}, \\
x_{4}+x_{5}+x_{1}=a_{4}, \\
x_{5}+x_{1}+x_{2}=a_{5} .
\end{array}\right.
$$
where $a_{1}, a_{2}, a_{3}, a_{4}, a_{5}$ are real constants, and $a_{1}>a_{2}>a_{3}>a_{4}>a_{5}$. Then the order of $x_{1}, x_{2}, x_{3}, x_{4}, x_{5}$ is
(A) $x_{1}>x_{2}>x_{3}>x_{4}>x_{5}$.
(B) $x_{4}>x_{2}>x_{1}>x_{3}>x_{5}$.
(C) $x_{3}>x_{1}>x_{4}>x_{2}>x_{5}$.
(D) $x_{5}>x_{3}>x_{1}>x_{4}>x_{2}$.
(China Junior High School Mathematics League, 1993)
|
C
|
11. The maximum value of the function $y=2 x+\sqrt{1-2 x}$ is
|
\frac{5}{4}
|
Find the sum of all $\left\lfloor x\right\rfloor$ such that $x^2-15\left\lfloor x\right\rfloor+36=0$.
$\text{(A) }15\qquad\text{(B) }26\qquad\text{(C) }45\qquad\text{(D) }49\qquad\text{(E) }75$
|
49
|
Problem 11.8. Real numbers $a, b, c$ are such that
$$
\left\{\begin{array}{l}
a^{2}+a b+b^{2}=11 \\
b^{2}+b c+c^{2}=11
\end{array}\right.
$$
(a) (1 point) What is the smallest value that the expression $c^{2}+c a+a^{2}$ can take?
(b) (3 points) What is the largest value that the expression $c^{2}+c a+a^{2}$ can take?
|
44
|
1. $\sqrt{1-\sin ^{2} 1997}-\sqrt{1-\cos ^{2} 1997}$ equals ).
(A) $\cos 1997-\sin 1997$
(B) $-\cos 1997-\sin 1997$
(C) $-\cos 1997+\sin 1997$
(D) $\cos 1997+\sin 1997$
|
D
|
## Task 2
Susanne estimated the length of the schoolyard to be $60 \mathrm{~m}$. Steffen and Ulf measure. They lay out a measuring tape of $20 \mathrm{~m}$ length twice and then measure another $14 \mathrm{~m}$.
By how many meters did Susanne overestimate?
|
6
|
2. In 6th grade class a, there are 24 students. Half of the students in this class play an instrument. Also, $\frac{5}{8}$ of the students in this class sing in the choir. If it is known that more than a third, but less than $\frac{5}{12}$ of the students in 6th grade class a both play an instrument and sing in the choir, how many students in this class neither play an instrument nor sing in the choir?
|
6
|
2・13 If the equation $(m+2) x^{2}-2(m+1) x+m=0$ has only one real root, then the equation $(m+1) x^{2}-2 m x+m-2=0$
(A) has no real roots.
(B) has two distinct real roots.
(C) has two equal real roots.
(D) the number of real roots cannot be determined.
(China "Zu Chongzhi Cup" Junior High School Mathematics Invitational Competition, 1995)
|
C
|
G2.1 一個盒子有五個球, 球面上分別印上號碼 3、4、6、9 或 10 。由盒中同時隨機取出 2 個球, 並得出其號碼的總和。若 $A$ 為不同總和的數量, 求 $A$ 的值。
A box contains five distinctly marked balls with number markings being $3,4,6,9$ or 10 . Two balls are randomly drawn without replacement from the box. If $A$ is the number of possible distinct sums of the selected numbers, determine the value of $A$.
|
9
|
Problem 2. A string with a length of $5 \mathrm{~m}$ is divided into equal parts with 4 cuts. From each part, a rectangle is formed such that the length is four times greater than the width. What is the length of the rectangle in cm?
|
40\mathrm{~}
|
13.035. A shoe factory completed $20 \%$ of the monthly plan in the first week, produced $120 \%$ of the amount of products made in the first week in the second week, and produced $60 \%$ of the products made in the first two weeks combined in the third week. What is the monthly production plan for shoes, if it is known that to complete it, it is necessary to manufacture 1480 pairs of shoes in the last week of the month?
|
5000
|
LI OM - I - Task 5
Determine all pairs $ (a,b) $ of natural numbers for which the numbers $ a^3 + 6ab + 1 $ and $ b^3 + 6ab + 1 $ are cubes of natural numbers.
|
(1,1)
|
13. The Youth Palace is recruiting for spring calligraphy, art, and music instrument classes. The calligraphy class has enrolled 29 students, among whom 13 are enrolled in both calligraphy and art, 12 are enrolled in both calligraphy and music instruments, and 5 are enrolled in all three subjects. Therefore, the number of students who only participate in calligraphy is $\qquad$.
|
9
|
9. As shown in the figure, the four vertices of square $A B C D$ are on the graphs of the inverse proportion functions $y=\frac{12}{x}$ and $y=\frac{20}{x}$ in the first quadrant, with the diagonals of the square parallel to the $x$-axis and $y$-axis, respectively. Then the x-coordinate of point $B$ is
|
4
|
We are given three non-negative numbers $A , B$ and $C$ about which it is known that $A^4 + B^4 + C^4 \le 2(A^2B^2 + B^2C^2 + C^2A^2)$
(a) Prove that each of $A, B$ and $C$ is not greater than the sum of the others.
(b) Prove that $A^2 + B^2 + C^2 \le 2(AB + BC + CA)$ .
(c) Does the original inequality follow from the one in (b)?
(V.A. Senderov , Moscow)
|
A^2 + B^2 + C^2 \le 2(AB + BC + CA)
|
$8.30 \log _{\frac{x-1}{x+5}} 0.3>0$.
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly.
However, the provided text is already in a mathematical form which is universally understood and does not require translation. The text in English remains:
$8.30 \log _{\frac{x-1}{x+5}} 0.3>0$.
|
(1,\infty)
|
[Helper area. The area helps solve the task] Pythagorean Theorem (direct and inverse) ]
Find the area of an isosceles triangle if the height dropped to the base is 10, and the height dropped to the side is 12.
|
75
|
8. Given real numbers $a, b$ satisfy
$$
a+\lg a=10, b+10^{b}=10 \text {. }
$$
Then $\lg (a+b)=$ $\qquad$
|
1
|
28. A rectangular prism with integer centimeter edge lengths has all 6 of its faces painted red, and then it is completely cut into small cubes with edge lengths of 1 centimeter. Among these small cubes, there are 24 cubes with exactly 1 face painted red, and 28 cubes with exactly 2 faces painted red. The original volume of the rectangular prism is $\qquad$ cubic centimeters.
|
60
|
# Problem 9.
Given a polynomial $P(x)$ of degree 10 with the leading coefficient 1. The graph of $y=P(x)$ lies entirely above the $O x$ axis. The polynomial $-P(x)$ is factored into irreducible factors (i.e., polynomials that cannot be expressed as the product of two non-constant polynomials). It is known that at $x=2020$, all the obtained irreducible polynomials take the value -3. Find $P(2020)$.
|
243
|
In the diagram, each small square is $1 \mathrm{~cm}$ by $1 \mathrm{~cm}$. The area of the shaded region, in square centimetres, is
(A) 2.75
(D) 4.5
(B) 3
(C) 3.25
(E) 6
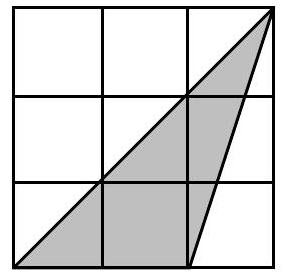
|
3
|
2.044. $\left(\frac{\sqrt{x-a}}{\sqrt{x+a}+\sqrt{x-a}}+\frac{x-a}{\sqrt{x^{2}-a^{2}}-x+a}\right): \sqrt{\frac{x^{2}}{a^{2}}-1} ; x>a>0$.
2.044. $\left(\frac{\sqrt{x-a}}{\sqrt{x+a}+\sqrt{x-a}}+\frac{x-a}{\sqrt{x^{2}-a^{2}}-x+a}\right): \sqrt{\frac{x^{2}}{a^{2}}-1} ; x>a>0$.
|
1
|
B2 The point $S$ lies on the chord $A B$ of a circle such that $S A=3$ and $S B=5$. The radius of the circle from the center $M$ through $S$ intersects the circle at $C$. Given $C S=1$.
Calculate the length of the radius of the circle.
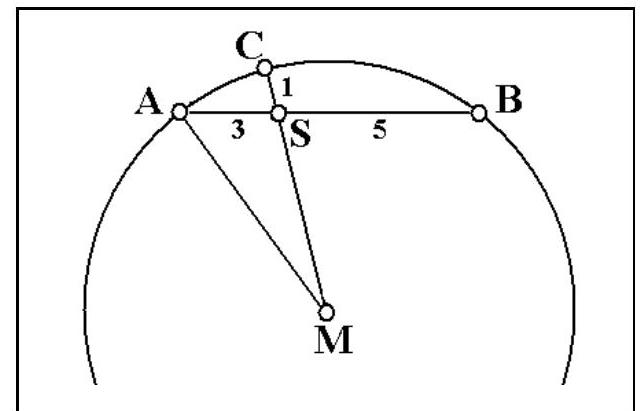
|
8
|
3. Find all integers $x, y$ for which $x+y, 2x+3y$ and $3x+y$ are perfect squares.
|
0
|
In the Cartesian plane is given a set of points with integer coordinate \[ T=\{ (x;y)\mid x,y\in\mathbb{Z} ; \ |x|,|y|\leq 20 ; \ (x;y)\ne (0;0)\} \] We colour some points of $ T $ such that for each point $ (x;y)\in T $ then either $ (x;y) $ or $ (-x;-y) $ is coloured. Denote $ N $ to be the number of couples $ {(x_1;y_1),(x_2;y_2)} $ such that both $ (x_1;y_1) $ and $ (x_2;y_2) $ are coloured and $ x_1\equiv 2x_2 \pmod {41}, y_1\equiv 2y_2 \pmod {41} $. Find the all possible values of $ N $.
|
420
|
## Task 4 - 180714
Determine the smallest prime number that leaves a remainder of 1 when divided by 5, 7, and 11!
|
2311
|
A7. If we paid a quarter of the debt, then half of the remainder, and an additional 5400 euros, the entire debt would be settled. How many euros are we in debt?
(A) 5400
(B) 9450
(C) 10800
(D) 14400
(E) 21600
|
14400
|
2. If $\frac{1-\cos \theta}{4+\sin ^{2} \theta}=\frac{1}{2}$, then $\left(4+\cos ^{3} \theta\right) \cdot\left(3+\sin ^{3} \theta\right)=$
|
9
|
In a country there are $n\geq 2$ cities. Any two cities has exactly one two-way airway. The government wants to license several airlines to take charge of these airways with such following conditions:
i) Every airway can be licensed to exactly one airline.
ii) By choosing one arbitrary airline, we can move from a city to any other cities, using only flights from this airline.
What is the maximum number of airlines that the government can license to satisfy all of these conditions?
|
\left\lfloor \frac{n}{2} \right\rfloor
|
Starting with a positive integer $n$, a sequence is created satisfying the following rule: each term is obtained from the previous one by subtracting the largest perfect square that is less than or equal to the previous term, until reaching the number zero. For example, if $n=142$, we will have the following sequence of 5 terms:
$$
a_{1}=142, a_{2}=21, a_{3}=5, a_{4}=1, a_{5}=0
$$
since $21=142-11^{2}, 5=21-4^{2}, 1=5-2^{2}$ and $0=1-1^{2}$.
a) Give an example of a sequence that has exactly 6 terms.
b) Find the smallest value of $n$ for which the sequence thus created has exactly 7 terms.
|
167
|
5 The number of roots of the equation $\left.a x^{2}+b|x|+c=0(a, b, c \in \mathbf{R}), a \neq 0\right)$ in the set of complex numbers is $n$, then
A. $n$ is at most 2
B. $n$ is at most 4
C. $n$ is at most 6
D. $n$ is at most 8
|
C
|
2. Calculate
$$
\frac{y^{2}+x y-\sqrt[4]{x^{5} y^{3}}-\sqrt[4]{x y^{7}}}{\sqrt[4]{y^{5}}-\sqrt[4]{x^{2} y^{3}}} \cdot(\sqrt[4]{x}+\sqrt[4]{y})
$$
where $x=3, \underbrace{22 \ldots 2}_{2013} 3, y=4, \underbrace{77 \ldots .7}_{2014}$. Choose the answer option with the number closest to the one you found.
|
8
|
19. Let
$$
F(x)=\frac{1}{\left(2-x-x^{5}\right)^{2011}},
$$
and note that $F$ may be expanded as a power series so that $F(x)=\sum_{n=0}^{\infty} a_{n} x^{n}$. Find an ordered pair of positive real numbers $(c, d)$ such that $\lim _{n \rightarrow \infty} \frac{a_{n}}{n^{d}}=c$.
|
(\frac{1}{6^{2011}2010!},2010)
|
29.44 The expression $21 x^{2}+a x+21$ can be factored into two linear factors, where $a$ is a positive integer. Then $a$ is
(A) any odd number.
(B) some odd number.
(C) any even number.
(D) some even number.
(E) zero.
(Shenzhen, Guangdong Province, China Junior High School Mathematics Competition, 1988)
|
D
|
32at8 ** Let $a, b, c \in \mathbf{R}^{+}, a+b+c=1$, find the minimum value of $\frac{a+3 c}{a+2 b+c}+\frac{4 b}{a+b+2 c}-$ $\frac{8 c}{a+b+3 c}$.
|
-17+12\sqrt{2}
|
Suppose that for the positive integer $n$, $2^{n}+1$ is prime. What remainder can this prime give when divided by $240$?
|
3,5,17
|
## Zadatak A-4.4.
Kružnica prolazi točkama $A(0,5)$ i $B(0,-1)$, a njeno središte pripada pravcu $y=2 x-6$. Odredi sinus obodnog kuta nad manjim lukom $\overparen{A B}$ te kružnice.
|
\frac{3}{5}
|
4. Find the smallest four-digit number, the product of all digits of which is equal to 512.
Answer. 1888
|
1888
|
Find all positive integers $a$ so that for any $\left \lfloor \frac{a+1}{2} \right \rfloor$-digit number that is composed of only digits $0$ and $2$ (where $0$ cannot be the first digit) is not a multiple of $a$.
|
3, 9
|
24. If $x^{2}+x-1=0$, find the value of $x^{4}-3 x^{2}+3$.
|
2
|
17. Suppose that the polynomial $P(x)=x^{3}+4 x^{2}+b x+c$ has a single root $r$ and a double root $s$ for some distinct real numbers $r$ and $s$. Given that $P(-2 s)=324$, what is the sum of all possible values of $|c|$ ?
|
108
|
$4 \cdot 44$ Let $a b \neq 0, a^{2}+b^{2}=1$, if
$$
X=\frac{a^{4}+b^{4}}{a^{6}+b^{6}}, \quad Y=\frac{a^{4}+b^{4}}{\sqrt{a^{6}+b^{6}}}, \quad Z=\frac{\sqrt{a^{4}+b^{4}}}{a^{6}+b^{6}} .
$$
then the size relationship of $X, Y, Z$ is
(A) $X<Y<Z$.
(B) $Y<Z<X$.
(C) $Y<X<Z$.
(D) $Z<X<Y$.
("Zu Chongzhi Cup" Junior High School Mathematics Invitational Competition, 1988)
|
C
|
8. Given a complex number $z$ satisfying $|z|=1$. Then
$$
f(z)=\left|z^{5}+\bar{z}^{3}+6 z\right|-2\left|z^{4}+1\right|
$$
the minimum value of $f(z)$ is $\qquad$
|
3
|
Problem 6. (30 points) A regular triangular prism $A B C A_{1} B_{1} C_{1}$ is inscribed in a sphere with the base $A B C$ and lateral edges $A A_{1}, B B_{1}, C C_{1}$. The segment $C_{1} D$ is the diameter of this sphere, and point $K$ is the midpoint of edge $C C_{1}$. Find the volume of the prism if $D K=2, D A=\sqrt{6}$.
|
2
|
Let $n\ge 2$ be a positive integer. Find the positive integers $x$
\[\sqrt{x+\sqrt{x+\ldots +\sqrt{x}}}<n \]
for any number of radicals.
|
1 \le x \le n^2 - n
|
A finite set of positive integers is called [i]isolated [/i]if the sum of the numbers in any given proper subset is co-prime with the sum of the elements of the set.
a) Prove that the set $A=\{4,9,16,25,36,49\}$ is isolated;
b) Determine the composite numbers $n$ for which there exist the positive integers $a,b$ such that the set
\[ A=\{(a+b)^2, (a+2b)^2,\ldots, (a+nb)^2\}\] is isolated.
|
n = 6
|
2. Find all real roots of the equation
$(x+1)^{5}+(x+1)^{4}(x-1)+(x+1)^{3}(x-1)^{2}+(x+1)^{2}(x-1)^{3}+(x+1)(x-1)^{4}+(x-1)^{5}=0$
|
0
|
Example 14 Let $a, b, c, a+b-c, a+c-b, b+c-a, a+b+c$ be seven distinct prime numbers, and the sum of two of $a, b, c$ is 800. Let $d$ be the difference between the largest and smallest of these seven prime numbers. Find the maximum possible value of $d$.
(2001, China Mathematical Olympiad)
|
1594
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.