problem
stringlengths 18
2.25k
| gt
stringlengths 1
173
|
|---|---|
Shapovalov A.V.
Each face of a cube $6 \times 6 \times 6$ is divided into $1 \times 1$ cells. The cube is covered with $2 \times 2$ squares such that each square covers exactly four cells, no squares overlap, and each cell is covered by the same number of squares. What is the maximum value that this identical number can take? (Squares can be bent over the edge.)
|
3
|
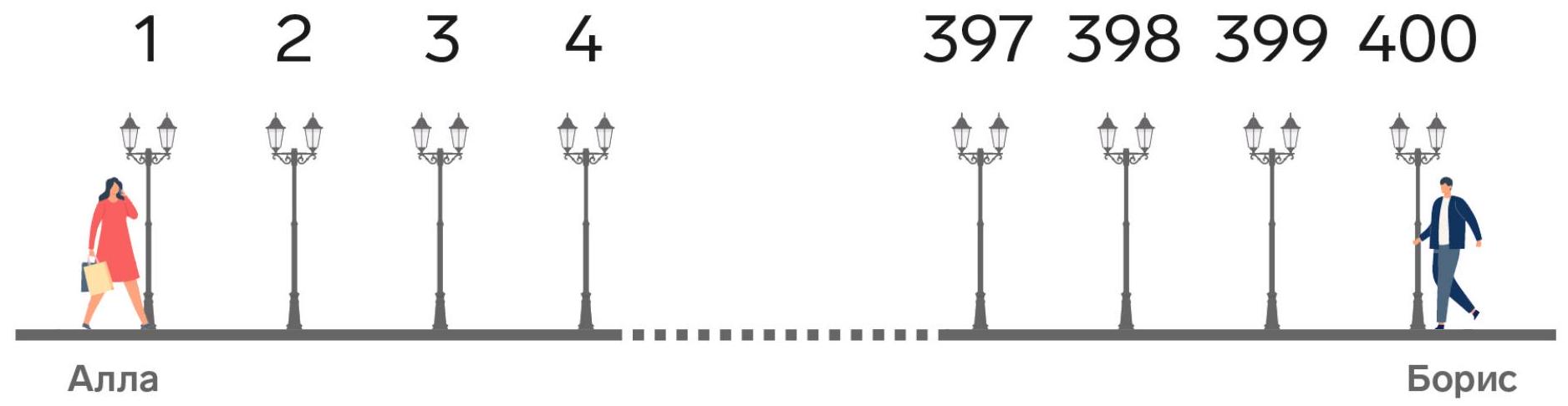
5-5. Along a straight alley, 400 lamps are placed at equal intervals, numbered in order from 1 to 400. At the same time, from different ends of the alley, Alla and Boris started walking towards each other at different constant speeds (Alla from the first lamp, Boris from the four hundredth). When Alla was at the 55th lamp, Boris was at the 321st lamp. At which lamp will their meeting occur? If the meeting occurs between two lamps, indicate the smaller number of these two.
|
163
|
3. Mowgli asked five monkeys to bring him some nuts. The monkeys collected an equal number of nuts and carried them to Mowgli. On the way, they quarreled, and each monkey threw one nut at each of the others. As a result, they brought Mowgli half as many nuts as they had collected. How many nuts did Mowgli receive? Be sure to explain your answer.
|
20
|
# 6. Variant 1
A doll maker makes one doll in 1 hour 45 minutes. After every three dolls made, the master has to rest for half an hour. Ten dolls are needed for gifts. At what time the next day (specify hours and minutes) will the order be completed if the master started making dolls at 10:00 AM and worked through the night?
|
5:00
|
6. Given $\sin \alpha>\sin \beta$, and $\alpha \neq k \pi+\frac{\pi}{2}, \beta \neq k \pi+\frac{\pi}{2},(\quad)$.
A. If $\alpha, \beta$ are angles in the first quadrant, then $\cos \alpha>\cos \beta$
B. If $\alpha, \beta$ are angles in the second quadrant, then $\tan \alpha>\tan \beta$
C. If $\alpha, \beta$ are angles in the third quadrant, then $\cos \alpha>\cos \beta$
D. If $\alpha, \beta$ are angles in the fourth quadrant, then $\tan \alpha>\tan \beta$
|
D
|
11. Guess the number. Sixth-graders Petya, Vasya, Kolya, and Anton made the following statements. Petya: “The number is prime.” Vasya: “The number is 9.” Kolya: “The number is even.” Anton: “The number is 15.” It is known that only one of Petya's and Vasya's statements is true, just as only one of Kolya's and Anton's statements is true. What number is guessed?
|
2
|
Example 1. What day of the week was October 1, 1949?
|
Saturday
|
Determine all possible values of $\frac{1}{x}+\frac{1}{y}$ if $x$ and $y$ are real numbers (not equal to $0$) that satisfy $x^{3}+y^{3}+3 x^{2} y^{2}=x^{3} y^{3}$.
|
-2 \text{ and } 1
|
5. The graph of the function $y=\sqrt{3} \cos x-\sin x$ is shifted to the left by $m$ units, and the resulting graph is symmetric about the $y$-axis. Then the smallest positive value of $m$ is ( ).
A. $\frac{\pi}{6}$
B. $\frac{\pi}{3}$
C. $\frac{2 \pi}{3}$
D. $\frac{5 \pi}{6}$
|
\frac{5\pi}{6}
|
1. For positive integers $n$, let $S_{n}$ be the set of integers $x$ such that $n$ distinct lines, no three concurrent, can divide a plane into $x$ regions (for example, $S_{2}=\{3,4\}$, because the plane is divided into 3 regions if the two lines are parallel, and 4 regions otherwise). What is the minimum $i$ such that $S_{i}$ contains at least 4 elements?
|
4
|
1. Decrypt the equation
$$
\overline{a b c d}=(5 c+1)^{2}
$$
|
1681
|
5. Express $(A-B)^{-1}$ in terms of $x$, if $A=\frac{3 x^{-\frac{1}{3}}}{x^{\frac{2}{3}}-2 x^{-\frac{1}{3}}}$ and $B=\frac{x^{\frac{1}{3}}}{x^{\frac{4}{3}}-x^{\frac{1}{3}}}$. Simplify the expression.
## You have 120 minutes to solve.
Solve each problem independently on the provided paper, with each problem on a separate page. Write only your code on the sheets. Write your answers in pen, clearly and neatly. Draw graphs with a pencil. If you solve a problem in multiple ways, clearly indicate which solution the evaluator should grade. If you make a mistake, strike it through.
Each solution will be graded on a scale of 0 to 6 points.
The National Competition Committee wishes you great success.
## 8th Mathematics Knowledge Competition for Students of Secondary Technical and Vocational Schools National Competition, April 19, 2008
## Problems for 3rd Year Students
|
\frac{(x-2)(x-1)}{2x-1}
|
For integer $n$, let $I_n=\int_{\frac{\pi}{4}}^{\frac{\pi}{2}} \frac{\cos (2n+1)x}{\sin x}\ dx.$
(1) Find $I_0.$
(2) For each positive integer $n$, find $I_n-I_{n-1}.$
(3) Find $I_5$.
|
\frac{1}{2} \ln 2 - \frac{8}{15}
|
3. (10 points) $A, B, C, D$ are assigned a permutation of the numbers $10, 20, 30, 40$, such that the value of the expression $\frac{1}{\mathrm{~A}-\frac{1}{B+\frac{1}{C-\frac{1}{D}}}}$ is maximized. Then the value of $A+2B+3C+4D$ is $\qquad$
Assign $A, B, C, D$ using a permutation of the numbers $10, 20, 30, 40$ to maximize the value of the expression $\frac{1}{\mathrm{~A}-\frac{1}{B+\frac{1}{C-\frac{1}{D}}}}$. Then, the value of $A+2B+3C+4D$ is $\qquad$
|
290
|
7.021. $3 \log _{5} 2+2-x=\log _{5}\left(3^{x}-5^{2-x}\right)$.
7.021. $3 \log _{5} 2+2-x=\log _{5}\left(3^{x}-5^{2-x}\right)$.
|
2
|
8. (10 points) Let for positive numbers $x, y, z$ the following system of equations holds:
$$
\left\{\begin{array}{l}
x^{2}+x y+y^{2}=27 \\
y^{2}+y z+z^{2}=16 \\
z^{2}+x z+x^{2}=43
\end{array}\right.
$$
Find the value of the expression $x y+y z+x z$.
|
24
|
192*. The sequence $\left(x_{n}\right)$ is defined by the conditions:
$$
x_{1}=\frac{1}{2}, \quad x_{n+1}=\sqrt{\frac{1-\sqrt{1-x_{n}^{2}}}{2}}
$$
Find a formula for $x_{n}$.
|
x_{n}=\sin\frac{\pi}{3\cdot2^{n}}
|
7. Given real numbers $a, b, c, d$ satisfy $5^{a}=4,4^{b}=3,3^{c}=2,2^{d}=5$, then $(a b c d)^{2018}=$
|
1
|
Šárka and Terezka received a box of chocolates, containing 35 chocolate candies. Each day, each of the girls ate at least one candy, and no candy was divided into parts. On the first day, Terezka ate $\frac{2}{5}$ of what Šárka ate on the same day. On the second day, Šárka ate $\frac{3}{4}$ of what Terezka ate on the same day. By the end of the second day, the box was empty.
How many candies did Terezka eat in total, given that the difference between the number of candies eaten by Terezka and the number of candies eaten by Šárka was the smallest possible?
(L. Hozová)
|
18
|
There are $5$ accents in French, each applicable to only specific letters as follows:
[list]
[*] The cédille: ç
[*] The accent aigu: é
[*] The accent circonflexe: â, ê, î, ô, û
[*] The accent grave: à, è, ù
[*] The accent tréma: ë, ö, ü
[/list]
Cédric needs to write down a phrase in French. He knows that there are $3$ words in the phrase and that the letters appear in the order: \[cesontoiseaux.\] He does not remember what the words are and which letters have what accents in the phrase. If $n$ is the number of possible phrases that he could write down, then determine the number of distinct primes in the prime factorization of $n$.
|
4
|
1. Calculate: $2019 \times 20182019-2018 \times 20192018=$
|
4037
|
Károly, László and Mihály went hunting for deer, foxes, and hares over three days. Each of them shot at least one of each type of game every day, and in total they shot 86 animals. On the first day, they shot 12 foxes and 14 deer, and on the second day, they shot a total of 44 animals. László shot an even number of each type of game every day, except for the second day when he shot 5 foxes. At the end of the hunt, Károly counted that they had shot 12 hares in total. Question: How many foxes did Mihály shoot on the third day?
|
1
|
8. $\alpha, \beta \in(0, \pi)$, and $\cos \alpha+\cos \beta-\cos (\alpha+\beta)=\frac{3}{2}$, then $2 \alpha+\beta=$
|
\pi
|
Example 1 Solve the equation $\sqrt[4]{10+x}+\sqrt[4]{7-x}=3$.
|
x_1=6, x_2=-9
|
$\left[\begin{array}{ll}{[\text { Ratio of volumes }}\end{array}\right]$
On the edges $B C, C D$ and $A D$ of the tetrahedron $A B C D$ with volume $V$, points $L, M$ and $N$ are taken respectively, such that $3 B L=B C$, $4 C M=C D$ and $5 D N=A D$. Find the volume of the tetrahedron $N M L B$.
|
\frac{V}{60}
|
17. The six-digit number $2 P Q R S T$ is multiplied by 3 and the result is the six-digit number PQRST2. What is the sum of the digits of the original number?
A 24
B 27
C 30
D 33
E 36
|
27
|
8.4. Point $E$ is the midpoint of side $A B$ of parallelogram $A B C D$. On segment $D E$, there is a point $F$ such that $A D = B F$. Find the measure of angle $C F D$.
|
90
|
4. Given the hyperbola $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1(a>0, b>0)$ with the right focus at $F$, the right directrix at $l$, and a line intersecting the two branches of the hyperbola at points $P$ and $Q$, and intersecting $l$ at $R$. Then ( ).
( A) $\angle P F R>\angle Q F R$
( B) $\angle P F R<\angle Q F R$
( C) $\angle P F R=\angle Q F R$
(D) The size of $\angle P F R$ and $\angle Q F R$ is uncertain
|
C
|
7.213. $\left|\log _{\sqrt{3}} x-2\right|-\left|\log _{3} x-2\right|=2$.
|
\frac{1}{9};9
|
11. Given real numbers $a, b$ satisfy
$$
\left\{\begin{array}{l}
a+b-2 \geqslant 0, \\
b-a-1 \leqslant 0, \\
a \leqslant 1 .
\end{array}\right.
$$
Then the maximum value of $\frac{a+2 b}{2 a+b}$ is $\qquad$
|
\frac{7}{5}
|
13. In a line, there are 20 numbers. It is known that the sum of any three consecutive numbers is greater than zero. Can we assert that the sum of all 20 numbers is greater than zero?
|
No
|
2. In a certain year, there are 5 Saturdays and 4 Sundays in October. Question: What day of the week was October 1st of that year?
|
Thursday
|
2. Let $n$ be a positive integer. If
$$
n \equiv r(\bmod 2)(r \in\{0,1\}) \text {, }
$$
find the number of integer solutions to the system of equations
$$
\left\{\begin{array}{l}
x+y+z=r, \\
|x|+|y|+|z|=n
\end{array}\right.
$$
|
3n
|
(5) If the set $A=\left\{z \left\lvert\, z=\frac{p}{q}\right., p+q=5, p, q \in \mathbf{N}^{*}\right\}$, then the set $A=$ $\qquad$ .
|
{\frac{1}{4},\frac{3}{2},\frac{2}{3},4}
|
Define $L(x) = x - \frac{x^2}{2}$ for every real number $x$. If $n$ is a positive integer, define $a_n$ by
\[
a_n = L \Bigl( L \Bigl( L \Bigl( \cdots L \Bigl( \frac{17}{n} \Bigr) \cdots \Bigr) \Bigr) \Bigr),
\]
where there are $n$ iterations of $L$. For example,
\[
a_4 = L \Bigl( L \Bigl( L \Bigl( L \Bigl( \frac{17}{4} \Bigr) \Bigr) \Bigr) \Bigr).
\]
As $n$ approaches infinity, what value does $n a_n$ approach?
|
\frac{34}{19}
|
4.079 Find the sum $\Sigma=1+2 \cdot 3+3 \cdot 7+\ldots+n\left(2^{n}-1\right)$.
|
(n-1)2^{n+1}+2-\frac{n(n+1)}{2}
|
12. Let $f: \mathbf{N}^{*} \rightarrow \mathbf{N}^{*}$, and for all $m, n \in \mathbf{N}^{*}$, we have $f(f(m)+f(n))=m+n$, then $f(2005)=$
|
2005
|
4. As shown in Figure 2, a chord $BC$ (not a diameter) of the semicircle $\odot O$ is used as the axis of symmetry to fold the arc $\overparen{BC}$, intersecting the diameter at point $D$. If $AD=4, BD=6$, then $\tan B=$ ( .
(A) $\frac{1}{2}$
(B) $\frac{2}{3}$
(C) $\frac{3}{4}$
(D) $\frac{4}{5}$
|
\frac{1}{2}
|
6. Connecting the diagonals of the regular pentagon $A_{1} A_{2} A_{3} A_{4} A_{5}$ intersects to form a regular pentagon $B_{1} B_{2} B_{3} B_{4} B_{5}$, and connecting the diagonals of the regular pentagon $B_{1} B_{2} B_{3} B_{4} B_{5}$ again intersects to form a regular pentagon $C_{1} C_{2} C_{3} C_{4} C_{5}$ (as shown in Figure 1). Then, among the triangles formed by the line segments in Figure 1, there are ( ) isosceles triangles.
(A) 50
(B) 75
(C) 85
(D) 100
|
C
|
8. When $a$ and $b$ are two distinct positive numbers, among the following three algebraic expressions:
$$
\begin{array}{l}
\text { A: }\left(a+\frac{1}{a}\right)\left(b+\frac{1}{b}\right), \\
\text { B: }\left(\sqrt{a b}+\frac{1}{\sqrt{a b}}\right)^{2}, \\
\text { C: }\left(\frac{a+b}{2}+\frac{2}{a+b}\right)^{2}
\end{array}
$$
the one with the largest value is
(A) definitely A;
(B) definitely B;
(C) definitely C;
(D) generally not certain, and depends on the values of $a$ and $b$.
|
D
|
Consider these two geoboard quadrilaterals. Which of the following statements is true?
$\text{(A)}\ \text{The area of quadrilateral I is more than the area of quadrilateral II.}$
$\text{(B)}\ \text{The area of quadrilateral I is less than the area of quadrilateral II.}$
$\text{(C)}\ \text{The quadrilaterals have the same area and the same perimeter.}$
$\text{(D)}\ \text{The quadrilaterals have the same area, but the perimeter of I is more than the perimeter of II.}$
$\text{(E)}\ \text{The quadrilaterals have the same area, but the perimeter of I is less than the perimeter of II.}$
|
E
|
1. The complex number $z$ satisfies
$$
|z-\mathrm{i}|=|z-1|=|z-2015| \text {. }
$$
Then $z=$ . $\qquad$
|
1008+1008
|
4.2. The line $p: y=-x+1$ and two points $\mathrm{A}(-1,5)$ and $\mathrm{B}(0,4)$ are given. Determine the point $P$ on the line $p$ for which the sum of the lengths of the segments $|A P|+|P B|$ is minimal.
|
(-2,3)
|
12. (2004 High School League - Liaoning Preliminary) The sum of the maximum and minimum values of the function $f(x)=\frac{\sqrt{2} \sin \left(x+\frac{\pi}{4}\right)+2 x^{2}+x}{2 x^{2}+\cos x}$ is $\qquad$ .
|
2
|
14 The number of ways to arrange 5 boys and 6 girls in a row such that girls can be adjacent to other girls but boys cannot be adjacent to other boys is $6!\times k$. Find the value of $k$.
|
2520
|
190. Among the numbers of the form $36^{k}-5^{l}$, where $k$ and $l$ are natural numbers, find the smallest in absolute value. Prove that the found number is indeed the smallest.
|
11
|
}
For which $n>3$ can a set of weights with masses $1,2,3, \ldots, n$ grams be divided into three equal-mass piles?
#
|
8
|
Example 9 Given that the sum of several positive integers is 1976, find the maximum value of their product. (IMO - 17 problem)
|
2\cdot3^{658}
|
64. Rearrange the digits of a three-digit number, the difference between the largest and smallest three-digit numbers obtained is exactly equal to the original three-digit number. This three-digit number is $\qquad$ .
|
495
|
7.4. How many zeros does the product $s(1) \cdot s(2) \cdot \ldots \cdot s(100)$ end with, where $s(n)$ denotes the sum of the digits of the natural number $n$?
|
19
|
1. Given real numbers $a, b, c$ satisfy
$$
\begin{array}{l}
a+b+c=1, \\
\frac{1}{a+b-c}+\frac{1}{b+c-a}+\frac{1}{c+a-b}=1 .
\end{array}
$$
Then $a b c=$
|
0
|
Auxiliary similar triangles [Thales' theorem and the theorem of proportional segments]
In triangle $ABC$, the bisector $AD$ divides side $BC$ in the ratio $BD: DC=2: 1$. In what ratio does the median from $C$ divide this bisector?
|
3:1
|
3. On the diagonal $BD$ of square $ABCD$, take two points $E$ and $F$, such that the extension of $AE$ intersects side $BC$ at point $M$, and the extension of $AF$ intersects side $CD$ at point $N$, with $CM = CN$. If $BE = 3$, $EF = 4$, what is the length of the diagonal of this square?
|
10
|
8.1. Large sandglasses measure an hour, and small ones measure 11 minutes. How can you use these sandglasses to measure a minute?
|
1
|
10.1. The first term of the sequence is 934. Each subsequent term is equal to the sum of the digits of the previous term, multiplied by 13. Find the 2013-th term of the sequence.
|
130
|
Question 69, The quadratic function $f(x)=x^{2}+m x+n$ has real roots, the inequality $s \leq(m-1)^{2}+(n-1)^{2}+$ $(m-n)^{2}$ holds for any quadratic function satisfying the above condition, then the maximum value of $s$ is $\qquad$ _.
|
\frac{9}{8}
|
In a 6-car metro train, there are 4 drunk passengers among the travelers. What is the probability that at most two cars have drunk passengers?
|
\frac{1}{6}
|
12. Given $A(\sqrt{\pi}, a) 、 B(\sqrt{\pi}, b)$ are two different points on the curve $y^{2}+x^{4}=2 x^{2} y+1$. Then the value of $|a-b|$ is ( ).
(A) 1
(B) $\frac{\pi}{2}$
(C) 2
(D) $\sqrt{1+\pi}$
(E) $1+\sqrt{\pi}$
|
2
|
2. Given that $\alpha$ is a root of the equation $x^{2}+x-\frac{1}{4}=0$, then the value of $\frac{\alpha^{3}-1}{\alpha^{5}+\alpha^{4}-\alpha^{3}-\alpha^{2}}$ is. $\qquad$ .
|
20
|
Problem 2. Find the number of the subsets $B$ of the set $\{1,2, \ldots, 2005\}$ having the following property: the sum of the elements of $B$ is congruent to 2006 modulo 2048 .
Emil Kolev
|
2^{1994}
|
The equation $x^3+6x^2+11x+6=0$ has:
$\textbf{(A)}\ \text{no negative real roots}\qquad\textbf{(B)}\ \text{no positive real roots}\qquad\textbf{(C)}\ \text{no real roots}\\ \textbf{(D)}\ \text{1 positive and 2 negative roots}\qquad\textbf{(E)}\ \text{2 positive and 1 negative root}$
|
B
|
If five squares of a $3 \times 3$ board initially colored white are chosen at random and blackened, what is the expected number of edges between two squares of the same color?
|
\frac{16}{3}
|
How many (possibly empty) sets of lattice points $\{P_1, P_2, ... , P_M\}$, where each point $P_i =(x_i, y_i)$ for $x_i
, y_i \in \{0, 1, 2, 3, 4, 5, 6\}$, satisfy that the slope of the line $P_iP_j$ is positive for each $1 \le i < j \le M$ ? An infinite slope, e.g. $P_i$ is vertically above $P_j$ , does not count as positive.
|
3432
|
11. I start at square " 1 ", and have to finish at square " 7 ", moving at each step to a higher numbered adjacent square.
How many possible routes are there?
A 7
B 9
C 10
D 11
E 13
|
13
|
3. (10 points) A certain three-digit number is a multiple of 2, adding 1 makes it a multiple of 3, adding 2 makes it a multiple of 4, adding 3 makes it a multiple of 5, and adding 4 makes it a multiple of 6. What is the smallest number that satisfies these conditions? $\qquad$ .
|
122
|
## Task B-2.1.
Solve the equation $\sqrt{3-\frac{1}{2020 x}}=1-\frac{1}{2020 x}$.
|
-\frac{1}{2020}
|
Example 2 Find all positive integer solutions $(x, y, z)$ for $8^{x}+15^{y}=17^{x}$.
|
(2,2,2)
|
8,9}
Chord $AB$ subtends an arc of a circle equal to $120^{\circ}$. Point $C$ lies on this arc, and point $D$ lies on chord $AB$. Given that $AD=2, BD=1, DC=\sqrt{2}$.
Find the area of triangle $ABC$.
#
|
\frac{3\sqrt{2}}{4}
|
A column of cars 300 m long is driving on the highway at a speed of 60 km/h. Passing by a police checkpoint, each car reduces its speed to 40 km/h. What will be the length of the column when all cars have passed the checkpoint?
#
|
200\mathrm{}
|
8. (10 points) Find the sum of the real roots of the equation
$$
2 \cdot 3^{3 x}-a \cdot 3^{2 x}-3(a+4) \cdot 3^{x}+18=0
$$
|
1
|
Example 4 Let real numbers $a, b$ satisfy
$$
3 a^{2}-10 a b+8 b^{2}+5 a-10 b=0 \text {. }
$$
Find the minimum value of $u=9 a^{2}+72 b+2$.
|
-34
|
4. If the sum of the squares of two pairs of opposite sides of a spatial quadrilateral are equal, then, the angle formed by its two diagonals is
|
90^{\circ}
|
1. Eight knights are randomly placed on a chessboard (not necessarily on distinct squares). A knight on a given square attacks all the squares that can be reached by moving either (1) two squares up or down followed by one squares left or right, or (2) two squares left or right followed by one square up or down. Find the probability that every square, occupied or not, is attacked by some knight.
|
0
|
Five. (Full marks 20 points) Let the constant $a>1>b>0$. Then, under what relationship between $a$ and $b$ is the solution set of $\lg \left(a^{x}-b^{x}\right)>0$ $(1, +\infty)$?
|
a=b+1
|
8. Given that the side faces of a regular tetrahedron are right triangles with an area of 1, then the volume of the regular tetrahedron is
|
\frac{\sqrt{2}}{3}
|
2. (4) At a round table, 2015 people are sitting. Every minute, any two people who are friends can swap places. It turns out that, after spending some time, the people at the table can sit in any order. What is the minimum number of pairs of friends among these 2015 people?
|
2014
|
4. If non-zero vectors $\boldsymbol{\alpha}, \boldsymbol{\beta}$ satisfy $|\boldsymbol{\alpha}+\boldsymbol{\beta}|=|\boldsymbol{\alpha}-\boldsymbol{\beta}|$, then the angle between $\boldsymbol{\alpha}$ and $\boldsymbol{\beta}$ is
|
90
|
Example 4 In hexagon $A B C D E F$, $\angle A=\angle B$ $=\angle C=\angle D=\angle E=\angle F$, and $A B+B C=$ $11, F A-C D=3$. Then $B C+D E=$ ?
(1994, Beijing Junior High School Mathematics Competition)
|
14
|
## Task 3
Inge buys 2 notebooks for 8 Pfennig each. Her friend needs twice as many notebooks. They pay together and put a 1 DM coin on the counter.
a) How many notebooks do the girls buy and how much do they pay for them?
b) How much money does the saleswoman give them back?
|
52
|
5. Let $E$ be a moving point inside square $ABCD$. It is known that the minimum value of the sum of the distances from $E$ to points $A$, $B$, and $C$ is $\sqrt{2}+\sqrt{6}$. Try to find the side length of this square.
|
2
|
Given a rectangle $A B C D$. Through point $A$ we draw a line that intersects segment $C D$ at point $X$ such that the areas of the resulting figures satisfy $S_{A X D}: S_{A B C X}=1: 2$. Through point $X$ we draw a line that intersects segment $A B$ at point $Y$ such that $S_{A X Y}: S_{Y B C X}=1: 2$. Finally, through point $Y$ we draw a line that intersects segment $X C$ at point $Z$ such that $S_{X Y Z}: S_{Y B C Z}=$ $=1: 2$.
Calculate the ratio of the areas $S_{A X D}: S_{A X Z Y}$.
|
9:10
|
Three. (Full marks 20 points) Let $a_{1}, a_{2}, \cdots$ and $b_{1}, b_{2}, \cdots$ be two arithmetic sequences, and their sums of the first $n$ terms are $A_{n}$ and $B_{n}$, respectively. It is known that for all $n \in N$, $\frac{A_{n}}{B_{n}}=\frac{2 n-1}{3 n+1}$. Try to write the expression for $\frac{a_{n}}{b_{n}}$ for all $n \in N$.
|
\frac{4 n-3}{6 n-2}
|
5.6. Among all the irreducible fractions, where the numerator and denominator are two-digit numbers, find the smallest fraction greater than $\frac{4}{9}$. In your answer, specify its numerator.
|
41
|
Let $B$ be the set of all binary integers that can be written using exactly $5$ zeros and $8$ ones where leading zeros are allowed. If all possible subtractions are performed in which one element of $B$ is subtracted from another, find the number of times the answer $1$ is obtained.
|
330
|
(Three, let $x \geqslant y \geqslant z \geqslant \frac{\pi}{12}$, and $x+y+z=\frac{\pi}{2}$. Find the maximum and minimum values of the product $\cos x \sin y \cos z$.
)
|
\frac{1}{8}
|
1. (12th "Hope Cup" Invitational Training Question) In the quadratic trinomial $a x^{2}+b x+c$, $a>100$, how many integer values of $x$ at most can make the absolute value of the quadratic trinomial not exceed 50?
|
2
|
G4.4 $A, B, C, D, E, F, G$ are seven people sitting around a circular table. If $d$ is the total number of ways that $B$ and $G$ must sit next to $C$, find the value of $d$.
|
48
|
A unit cube is cut twice to form three triangular prisms, two of which are congruent, as shown in Figure 1. The cube is then cut in the same manner along the dashed lines shown in Figure 2. This creates nine pieces. What is the volume of the piece that contains vertex $ W$?
[asy]import three;
size(200);
defaultpen(linewidth(.8pt)+fontsize(10pt));
currentprojection=oblique;
path3 p1=(0,2,2)--(0,2,0)--(2,2,0)--(2,2,2)--(0,2,2)--(0,0,2)--(2,0,2)--(2,2,2);
path3 p2=(2,2,0)--(2,0,0)--(2,0,2);
path3 p3=(0,0,2)--(0,2,1)--(2,2,1)--(2,0,2);
path3 p4=(2,2,1)--(2,0,0);
pen finedashed=linetype("4 4");
draw(p1^^p2^^p3^^p4);
draw(shift((4,0,0))*p1);
draw(shift((4,0,0))*p2);
draw(shift((4,0,0))*p3);
draw(shift((4,0,0))*p4);
draw((4,0,2)--(5,2,2)--(6,0,2),finedashed);
draw((5,2,2)--(5,2,0)--(6,0,0),finedashed);
label("$W$",(3,0,2));
draw((2.7,.3,2)--(2.1,1.9,2),linewidth(.6pt));
draw((3.4,.3,2)--(5.9,1.9,2),linewidth(.6pt));
label("Figure 1",(1,-0.5,2));
label("Figure 2",(5,-0.5,2));[/asy]$ \textbf{(A)}\ \frac {1}{12}\qquad \textbf{(B)}\ \frac {1}{9}\qquad \textbf{(C)}\ \frac {1}{8}\qquad \textbf{(D)}\ \frac {1}{6}\qquad \textbf{(E)}\ \frac {1}{4}$
|
\frac{1}{12}
|
19. Amy, Becky and Chloe went shopping. Becky spent only $15 \%$ of what Chloe spent. However, Amy spent $60 \%$ more than Chloe. Together they spent $£ 55$. How much did Amy spend?
A $£ 3$
B $£ 20$
C $£ 25$
D $£ 26$
E $£ 32$
|
32
|
Let $n$ be an integer greater than two, and let $A_1,A_2, \cdots , A_{2n}$ be pairwise distinct subsets of $\{1, 2, ,n\}$. Determine the maximum value of
\[\sum_{i=1}^{2n} \dfrac{|A_i \cap A_{i+1}|}{|A_i| \cdot |A_{i+1}|}\]
Where $A_{2n+1}=A_1$ and $|X|$ denote the number of elements in $X.$
|
n
|
Problem 5.3. A cuckoo clock is hanging on the wall. When a new hour begins, the cuckoo says "cuckoo" a number of times equal to the number the hour hand points to (for example, at 19:00, "cuckoo" sounds 7 times). One morning, Maxim approached the clock when it was 9:05. He started turning the minute hand until he advanced the clock by 7 hours. How many times did "cuckoo" sound during this time?

|
43
|
Which of the followings gives the product of the real roots of the equation $x^4+3x^3+5x^2 + 21x -14=0$?
$
\textbf{(A)}\ -2
\qquad\textbf{(B)}\ 7
\qquad\textbf{(C)}\ -14
\qquad\textbf{(D)}\ 21
\qquad\textbf{(E)}\ \text{None of the preceding}
$
|
-2
|
For a given value of $k$ the product of the roots of $x^2-3kx+2k^2-1=0$
is $7$. The roots may be characterized as:
$\textbf{(A) }\text{integral and positive} \qquad\textbf{(B) }\text{integral and negative} \qquad \\ \textbf{(C) }\text{rational, but not integral} \qquad\textbf{(D) }\text{irrational} \qquad\textbf{(E) } \text{imaginary}$
|
\textbf{(D)}
|
4. In the rectangle $A B C D$, point $M$ lies on side $C D$ and it holds that $D M=2 \cdot C M$, and $O$ is the intersection of the diagonals. The lines $A C$ and $B M$ intersect at a right angle. Determine $\measuredangle B O M$.
|
90
|
In an isosceles triangle with angles $\alpha, \beta, \gamma$. What are these angles if $\sin ^{2} \alpha+\sin ^{2} \beta=\sin \gamma$?
|
\alpha=\beta=45,\gamma=90
|
Aerith thinks $(1.4)^{(1.4)^{(1.4)}}$ is well-defined, but Bob thinks it diverges. Who is right?
|
Aerith
|
Example 2 If $f(x) (x \in \mathbf{R})$ is an even function with a period of 2, and when $x \in [0,1]$, $f(x) = x^{\frac{1}{19988}}$, then the ascending order of $f\left(\frac{98}{19}\right), f\left(\frac{101}{17}\right), f\left(\frac{104}{15}\right)$ is
|
f\left(\frac{101}{17}\right)<f\left(\frac{98}{19}\right)<f\left(\frac{104}{15}\right)
|
59. If the product of 5 consecutive natural numbers is 360360, then the middle number of these 5 consecutive natural numbers is
$\qquad$
|
13
|
4 $[\quad$ Equifacetal Tetrahedron $\quad]$
In the triangular pyramid $A B C D$, the sums of the three dihedral angles at each of the vertices $B$ and $C$ are $180^{\circ}$ and $A D=B C$. Find the volume of the pyramid if the area of the face $B C D$ is 100, and the distance from the center of the circumscribed sphere to the plane of the base $A B C$ is 3.
|
400
|
1. The monotonic decreasing interval of the function $y=\log _{\frac{1}{5}}|x-2|$ is ( ).
A. $(-\infty, 2)$
B. $(-\infty,-2) \cup(2,+\infty)$
C. $(2,+\infty)$
D. $(0,2) \cup(2,+\infty)$
|
C
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.